This page was generated from the Jupyter notebook compare_whittaker.ipynb.

Comparison: Numerov - Whittaker

This notebook compares the Numerov method (with and without model potentials) to the Whittaker method for calculating Rydberg wavefunctions and matrix elements.

import logging

import matplotlib.pyplot as plt
import numpy as np

from rydstate import RydbergStateAlkali

logging.basicConfig(level=logging.INFO, format="%(levelname)s %(filename)s: %(message)s")

Wavefunction

states: dict[str, RydbergStateAlkali] = {}

state = RydbergStateAlkali("Rb", n=21, l=0, j=0.5)

state.radial.create_model(potential_type="model_potential_marinescu_1993")
state.radial.create_wavefunction("numerov")
states["Numerov with Model Potentials"] = state

# Using Numerov without model potentials will lead to some warnings,
# since the resulting wavefunction does not pass all heuristic checks
state_without_mp = RydbergStateAlkali(state.species, state.n, state.l, state.j)
state_without_mp.radial.create_model(potential_type="coulomb")
state_without_mp.radial.create_wavefunction("numerov")
states["Numerov without Model Potentials"] = state_without_mp

WARNING wavefunction.py: The wavefunction for the state RadialState(Rb, n=21, nu=np.float64(17.86825962895559), l_r=0) has some issues:
      The wavefunction is not close to zero at the inner boundary (inner_weight_scaled_to_whole_grid=1.24e-04)
      The wavefunction has 17 nodes, but should have 20 nodes.
      The integration for l=0 did stop at 0.14 (should be close to zero).

state_whittaker = RydbergStateAlkali(state.species, state.n, state.l, state.j)
state_whittaker.radial.create_grid(x_min=state.radial.grid.x_min, x_max=state.radial.grid.x_max)
state_whittaker.radial.create_wavefunction("whittaker")
states["Whittaker"] = state_whittaker

WARNING wavefunction.py: Using Whittaker to get the wavefunction is not recommended! Use this only for comparison.

fig, ax = plt.subplots()
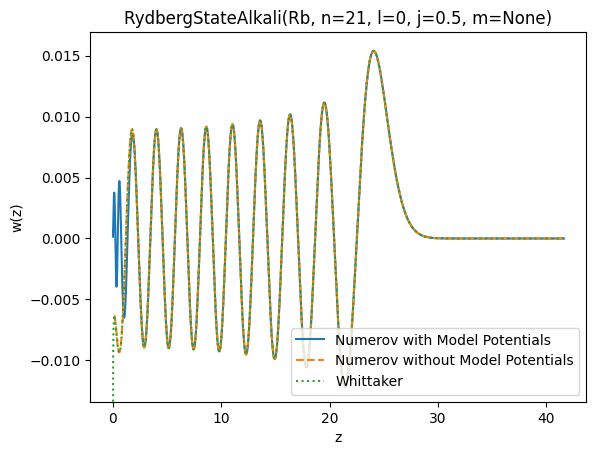
ax.set_title(str(state))

styles = ["-", "--", ":"]
for i, (label, _state) in enumerate(states.items()):
    ax.plot(_state.radial.grid.z_list, _state.radial.wavefunction.w_list, ls=styles[i], label=label)
ax.legend()

ax.set_xlabel("z")
ax.set_ylabel("w(z)")

ax.set_ylim(1.1 * np.min(state.radial.wavefunction.w_list), 1.1 * np.max(state.radial.wavefunction.w_list))

plt.show()

Radial matrix elements

state1 = RydbergStateAlkali("Rb", n=10, l=0, j=0.5)
state2 = RydbergStateAlkali("Rb", n=9, l=1, j=1.5)

dipole_me = state1.radial.calc_matrix_element(state2.radial, 1)
print(f"Numerov with model potentials: {dipole_me}", flush=True)

_state1 = RydbergStateAlkali(state1.species, state1.n, state1.l, state1.j)
_state1.radial.create_model(potential_type="coulomb")
_state2 = RydbergStateAlkali(state2.species, state2.n, state2.l, state2.j)
_state2.radial.create_model(potential_type="coulomb")

dipole_me = _state1.radial.calc_matrix_element(_state2.radial, 1)
print(f"Numerov without model potentials: {dipole_me}", flush=True)

# For Whittaker we use the same integration bounds as Numerov without model potentials,
# to avoid integrating over the diverging peak at the origin (see plots above)
xmin1, xmax1 = _state1.radial.grid.x_min, _state1.radial.grid.x_max
xmin2, xmax2 = _state2.radial.grid.x_min, _state2.radial.grid.x_max
_state1 = RydbergStateAlkali(state1.species, state1.n, state1.l, state1.j)
_state1.radial.create_grid(x_min=xmin1, x_max=xmax1)
_state1.radial.create_wavefunction("whittaker")
_state2 = RydbergStateAlkali(state2.species, state2.n, state2.l, state2.j)
_state2.radial.create_grid(x_min=xmin2, x_max=xmax2)
_state2.radial.create_wavefunction("whittaker")

dipole_me = _state1.radial.calc_matrix_element(_state2.radial, 1)
print(f"Whittaker: {dipole_me}", flush=True)

Numerov with model potentials: 43.64042739463778 bohr

WARNING wavefunction.py: The wavefunction for the state RadialState(Rb, n=10, nu=np.float64(6.864783105371448), l_r=0) has some issues:
      The wavefunction has 6 nodes, but should have 9 nodes.
      The integration for l=0 did stop at 0.14 (should be close to zero).
WARNING wavefunction.py: The wavefunction for the state RadialState(Rb, n=9, nu=np.float64(6.350837333725099), l_r=1) has some issues:
      The wavefunction is not close to zero at the inner boundary (inner_weight_scaled_to_whole_grid=4.07e-02)
      The wavefunction has 5 nodes, but should have 7 nodes.

Numerov without model potentials: 43.60588874251313 bohr

WARNING wavefunction.py: Using Whittaker to get the wavefunction is not recommended! Use this only for comparison.
WARNING wavefunction.py: Using Whittaker to get the wavefunction is not recommended! Use this only for comparison.

Whittaker: 43.56160364558853 bohr